تناسبات در معماری 25 صفحه – تناسبات هندسی و طلائی در معماری – معماری
عنوان : تناسبات در معماری
موضوع : تناسبات هندسی و طلائی در معماری
ارسال شده از : آرشیو سایت
تناسبات در معماری
چکیده :
آنچه در این مقاله بیان می شود برداشتی از بررسی و مقایسه هنر و ریاضی وکاربرد ریاضی در هنر است.
هر پدیده زیبا در طبیعت می تواند از دو نظر مورد توجه قرار بگیرد، هم از نگاه هنری وهم از دید ریاضی ونظم منطقی .هنر و ریاضی همانند یکدیگرند، زیرا در هردو مفاهیم تناسب ، تقارن و توازن نقش مهمی دارند.
هنرمندان معمولاً محدوده و فضای اثر هنری خود را از یک طرح ریاضی انتخاب می کنند .به طور کلی ترسیم هر شکل نیازمند بعضی ترسیمات کمکی است که به وسیله آنها نقاط ، خطوط ویا سطوح آن شکل تعریف می گردد.مفاهیم سطح و حجم چه در ریاضی و چه در هنر بسیار مورد استفاده قرار می گیرند.
امیدوارم از این پروژه که از آرشیو سایت ارسال شده راضی باشید.
از همینجا از شما عزیزان درخواست دارم هر اطلاعاتی که در ارتباط با رشته معماری و عمران در اختیار دارید برایم ارسال کنید تا با نام خودتان در سایت انتشار بدم و بقیه دوستان هم استفاده کنند.
برای دانلود به ادامه مطلب بروید…
![]() توضیحات : تناسبات در معماری – تناسبات هندسی و طلائی در معماری – معماری
توضیحات : تناسبات در معماری – تناسبات هندسی و طلائی در معماری – معماری
مقدمه
انسان همواره با تلاش خستگی ناپذیر رو به سوی کمال خویش دارد، بیش از آنچه هست طلب می کند.عقاب خیا ل و اندیشه خویش را تا دورترین نقاط افلاک و کاینات به پرواز در می آورد ودل هر ذره را می شکافد تا به جهانی از نا شناخته ها دست یابد و جهان را زیر سیطره قدرت خویش کشد.و همچنان نا آرام و بی قرار از آنچه هست، ناراضی می ماند.
انسان، زمانی انسان شد که به کمک دستان خود، کارکردن با اشیا طبیعی را فرا گرفت و به ساختن ابزار پرداخت . انسان ابزار ساز با دست آفریده ی خویش ، موجودیتی نو یافت و راه به سوی تکامل گشود . در این مسیر تکامل فکری ، بشر موفق شد ،به جای استفاده از اشیا ء که در طبیعت مشابه آن ها یافت نمی شد . و این نشانی است از زایش قدرت آفرینندگی در ذهن انسان پیش از تاریخ ، و از این رو انسان دیگر برای برتری و استیلا بر طبیعت ، به نیروی نامحدودی دست یافت که هنر یکی از بارزترین و شکوه مند ترین جلوه های آن به شمار می رود . حال سؤال این است که آیا هنر به تنهایی کافی است که انسان بتواند از خود دست آفریده های هنری به یادگار بگذارد ؟
اگر این را بپذیریم که ، تصور و خیال ، یکی از سر چشمه های اصلی آفرینش های هنری است آن وقت ناچاریم قبول کنیم که در ریاضیات هم ، دست کم عنصر های زیبایی و هنر وجود دارد چرا که مایه ی اصلی کشف های ریاضی ، همان تصور و خیال است .
با هیچ نیرنگی ، نمی توان از کشش انسان ها به سمت زیبایی ها جلوگیری کرد و آن چه زشت و نا زیبا است را جانشین زیبایی ها کرد
« رودن » مجسمه ساز مشهور فرانسوی می گوید : «من یک رویا پرداز نیستم بلکه یک ریاضی دان ام . مجسمه های من تنها به خاطر این خوب اند که ساخته و پرداخته ی اندیشه ی ریاضی اند . »
هر انسانی از تماشای چشم انداز یک دامنه ی سر سبز آرامش خود را با زمی یابد ، در عین حال به فکر فرو می رود . نقاش با قلم و بوم خود تلاش می کند که دیگران را در شادی خود شریک کند و ریاضی دان نحوه ی قرار گرفتن گل و گلبرگ ها یا اندازه و شکل ها را مورد مطالعه قرار می دهد . ولی هم گیاه عضوی یگانه است و هم انسان و اگر بخواهیم برخورد انسان با گیاه را بررسی کنیم ناچاریم ، به همه ی این جنبه ها توجه داشته باشیم .
ارتباط ریاضی با هنر
در دوران رنسانس ، نقاشان بزرگ ، ریاضی دانان هم بودند . آلبرتی نخستین نیاز نقاش را هندسه می دانست . او بود که در سال ۱۴۳۵ میلادی ، اولین کتاب را درباره پرسپکتیو نوشت . نقاشان و هنرمندان برای جان دادن به تصویر ها و القای فضای سه بعدی به آثار خود ، به ریاضیات روی آ ورند . بنابراین همه ی نقاشان دوره رنسانس نظیر آلبرتی ، دیودر ، لئوناردو داوینچی ، ریاضی دانان هنرمند یا هنرمندانی ریاضی دان بودند .
طبیعت ، سرچشمه زاینده و بی پایانی است برای انگیزه دادن به هنرمند و ریاضی دان . آن ها از درون خود و از ایده ها سود میجویند و حقیقت را نه تنها آن گونه که مشاهده می شود ، بلکه آن که باید باشد و آرزوی آدمی است ، می بینند . هنر و ریاضیات هر دو کمال و ایده ال را می جویند . در واقع تمامی عرصه ریاضیات سرشار از زیبایی و هنر است . زیبایی ریاضیات را می توان در شیوه بیان موضوع ، در طرز نوشتن و آرا یه آن در استدلال ها منطقی آن ، در رابطه آن بازندگی و واقعیت ، در سرگذشت پیدایش و تکامل آن و در خود موضوع ریاضیات مشاهده کرد یکی از راه های شناخت زیبایی های ریاضیات ( به خصوص هندسه ) آگاهی بر نحوه پیشرفت و تکامل است . جنبه دیگری از زیبایی ریاضیات این است که با همه انتزاعی بودن خود ، بر همه دانش ها حکومت می کند و جز قانون های آن ، هم چون ابزار نیرو مند دانش های طبیعی و اجتماعی را صیقل می دهد ، به پیش می برد . تفسیر می کند ودر خدمت انسان قرار می دهد .
ریاضی دان انگلیسی«ج.ه.هاردی » معتقد است : معیار ریاضی دان مانند معیار نقاش یا شاعر ،زیبایی است . اندیشه ها هم مانند رنگها یا وا ژه هاباید در هماهنگی کامل و سازگار با یکدیگر باشند . زیبایی نخستین معیار سنجش است .
همیلتون ریاضی دان ایرلندی در یکی از سخنرانی های خود در ارتباط با نجوم گفته است : «هنر و ریاضیات همانند یک دیگرند ، زیرا در هر دو مفاهیم تناسب ، تقارن و توازن نقش مهمی دارند . »
انیشتین می گوید : « تخیل مهم تر از معلومات است » که منظور تخیلات واهی نیست بلکه تفکر و ادیشه در مسائل و مفاهیم علمی است که باعث خلاقیت می شود .
به قول شاعر که می گوید :
« میاسای از اندیشه گونگون که دانش ز اندیشه گردد فزون »
هر چیز که در طبیعت زیبا جلوه کند می توان هم به دید ریاضی و هم به دید هنر به آن نگاه کرد و از طرفی می توان ملاحظه کرد که ریاضی هم می تواند به صورت یک هنر جلوه کند. یک اثبات زیبا برای یک مسئله یا قضیه ی ریاضی ازدید یک ریاضی دان یک هنر است پس با کمی دقت ملاحظه میشود که هنر وریاضی کاملا″ قابل مقایسه می باشند که ریاضی یک هنر بدیع وهنر قابل بیان به زبان ریاضی است.
در این جا لازم است به نکته ای توجه کنیم که گاهی عواطف انسانی در جلوه ی زیبایی تاثیر گذار باشد این تفکر ایجاد شود که حتی مثال نقضی برای تعریف هنر باشد در صورتی که چنین نیست و همان طور که در تعریف هنر از دید هنرشناسان بیان شده لزوما″معیارهای زیبایی ازدیدگاه های مختلف ممکن است یکی نباشد ولی با تعریف کلی مطابقت دارد.همچنین افرادی در یک هنر تخصص نداشته باشند زیبایی آن هنر برای این افراد قابل درک نیست . به عنوان مثال زیبایی که یک هنرمند نقاش در تابلوی معروف لبخند ژوکوند اثر لئوناردوداوینچی می بیند برای کسی که با هنر نقاشی و سبک این نقاشی آشنا نباشد متفاوت است . در همین رابطه و جلوه های زیبایی ریاضی می توان به اثبات آخرین قضیه ی فرما اشاره کرد که توسط اندره وایلد و شمورا انجام شد که یک شاهکار
هنری قرن بیستم برای ریاضی دانان می باشد پس ملاحظه می شود که هنر و ریاضیات در مفهوم کلی کاملا″ قابل مقایسه اند.
کادر در هنر
کادر یا قاب تصویر محدوده ی فضا یا سطحی است که اثر تجسمی در آن ساخته می شود . به طور کلی منظور از کادر در هنرهایی که با سطح سر و کار دارند و بر سطح به وجود می آیند همان محدودهای است که هنرمند برای ارائه و اجرای اثر خود بر می گزینند .
کادر می تواند اندازه ها و شکل های گونا گونی داشته باشد مثل انواع چهار گوش با ابعاد و تناسبات مختلف به صورت مربع و مستطیل های متنوع عمودی و افقی .هم چنین شکل های دیگر هندسی مثل دایره ، بیضی ، مثلث یا حتی تلفیقی از این اشکال به صورت منظم و غیر منظم به کار عنوان کادر به گرفته می شوند .
هنر مندان معمولا″ ترکیب عناصر و نیرو های بصری کار خود را براساس کادر و فضای بصری ، که در اختیار دارند ، سازماندهی می کنند محدوده و فضای اثر هنری به هر شکل که انتخاب شود در تأثیر گذاری بر نیرو های بصری و ترکیب آن ها با یک دیگر مؤثر است . کادر های هندسی مثل انواع چهار گوش ، سه گوش و دایره محدوده ای هستند که اثر تجسمی در آن ها به وجود می آید .
نقطه : نقطه از دیدگاه ریاضی ، عنصری است که هیچ گونه بعدی ندارد ، فضایی را اشغال نمی کند ، در ابتدا و انتهای هر خط قرار دارد و بالاخره از تقاطع و تماس دو خط به وجود می آید و نقطه موضوعی ذهنی است که در فضا یا بر صفحه تصور می شود ، بدون این که قابل دیدن و لمس شدن باشد . اما این مفهوم ذهنی وقتی بخواهد نشان داده شود با استفاده از یک ابزار اثر گذار مشخص می شود که در این صورت تبدیل به یک نقطه بصری خواهد شد . مثل نشان دادن مرکز یک دایره یا محل تقاطع دو پاره خط ، یا وقتی بخواهیم خطی را بر صفحه ای ترسیم کنیم اولین تماس ابزار ما با صفحه یک نقطه خواهد بود .
خط
خط از دید گاه ریاضی از به هم پیوستن نقطه ها به وجود می آید دارا ی طول اما فاقد عرض است ، نشان دهنده جهت و موقعیت است . و مرز سطح را شکل می دهد و آن را محدود می کند . خط عنصر اصلی طراحی است که در جریان آفرینش هنرهای تجسمی نقشی اساسی را ایفا می کند . خط اغلب بیان کننده عواطف واحساسات و نشانگر تفکر و اندیشه و آرمان های ذهنی هنرمند است .
خط به عنوان وسیله ی اصلی طراحی برای نمایش دادن ،شکل، ایجاد تیرگی وحجم نمایی به کار می رود. یک طراحی معمولا″در مرحله ای دیگر برای ساختن نقاشی استفاده می شود.
سطح
شکلی که دارای دو بعد باشد سطح نامیده می شود. همچنین روی چیزها را نیز سطح می گویند. همه ی سطح ها از سه شکل هندسی دایره ، مربع ، مثلث یا ترکیبی از آنها به وجود می آیند .
دایره شکل کاملی است که حرکت جاودانه و مداومی را نشان می دهد ،آسمان بلند که شعرا به آن دایره مینایی می گویند همه و همه نشان دهنده تناسبی است که میان شکل دایره و اشکال متنوع طبیعت وجود دارد بسیاری از هنر مندان به ویژه در هنر ایرانی نقاشان بزرگ برای ساختن آثار خود از ترکیبهایی بر اساس دایره و چرخشی الهام گرفته اند.
مربع یکی دیگر از شکل های پایه و ساده ی هندسی است ، از تغییرات زاویه ها و ضلع های مربع اشکال چهار گوش متنوعی به وجود می آید این شکل مظهر قدرت زمین و مادی و در عین حال اززیباترین اشکال هندسی است و نماد صلابت ، استحکام و سکون است.
مثلث متساوی الاضلاع نیز دارای سه ضلع و سه زاویه مساوی است هنگامی که این شکل بر سطح قاعده اش قرار بگیرد پایدارترین شکل هندسی است و مثل یک کوه استوار به نظر می رسد.مثلث به واسطه زوایای تندی که دارد سطحی مهاجم و شکلی ستیزنده به نظر می رسد که همواره در حال تحول و پویایی است .استفاده از مثلث و شبکه های مثلثی یک اصل ساختاری در طبیعت به شمار می رود.
از تکرار و ترکیب شکل های مثلث ، مربع و دایره می توان سطح های متعدد منظم و غیر منظمی به دست آورد همچنان اگر ا
شکال پیچیده و آلی طبیعت را تجزیه و ساده کنیم مجدداً به ا شکال ساده دایره، مثلث و مربع خواهیم رسید .
حجم
به چیزهایی که دارای سه بعد : طول و عرض و ارتفاع یا عمق باشند حجم گفته می شود معمولاً همه اشیاء مادی در طبیعت ،
دارای حجم هستند .این حجم ها گاهی به طور طبیعی به صورت نسبتاً منظمی دیده می شوند . مثل حجم برخی از درختها ،
میوه ها و تخم پرند گان و جانوران ، اما بیشتر اوقات به شکل غیر منظم جلوه می کنند ، مثل حجم صخره ها ، گیاهان ، حیوانات و بسیاری چیزهای دیگر .
همان طور که سه شکل دایره ،مربع ومثلث به عنوان اشکال پایه برای سطح نام برده شدند ، دایره ،مکعب و هرم را نیز می توان به عنوان اجسام هندسی پایه نام برد. این سه نوع حجم به طور کاملاً منظم به ندرت در طبیعت دیده می شوند . اما به طور کلی همه ی حجم های طبیعت از ترکیب یا تغییر شکل این سه حجم پایه و هندسی به وجود می آیند .
ازچرخش یک مثلث به دور محور عمودی خودش حجمی به وجود می آید که به آن مخروط گفته میشود. از حرکت دورانی سطوح مربع و مستطیل شکل نیز استوانه ای حاصل می شود که دارای سه سطح تحتانی ،بالایی وجانبی است .از چرخش دایره نیز به دور محور قطری خودش حجم کره ساخته می شود.
نمایش حجم در فضا و روابط متقابل آن با فضای پیرامونش اصل مهم مجسمه سازی است. این روابط در نقش برجسته سازی که از یک سو با نقاشی و از سوی دیگر با معماری در ارتباط است اهمیتی به سزا دارد.
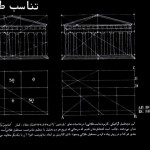
تئوری های تناسبات
منظور از تئوری های تناسبات ٬ ایجاد احساس نظم بین اجزاء یک ترکیب بصری است.
طبق نظریه ” اقلیدس ” نسبت ٬ به مقایسه کمی دو چیز مشابه اطلاق می شود ٬ حال آنکه تناسب به تساوی نسبتها اطلاق می شود .
بنابراین ٬ تحت هر سیستم تنظیم تناسب عمل کردن ٬ به معنی در نظر گیری یک نسبت اختصاصی است و این کیفیت ثابتی است که از یک نسبت به نسبت دیگر منتقل می شود .
بدین ترتیب ٬ سیستم تنظیم تناسب ٬ مجموعه ای از نسبتهای ثابت بصری را بین اجزاء یک بنا و نیز بین اجزاء و کل بوجود می آورد .
با اینکه این نسبتها در نظر اول ممکن است به چشم بیننده ای که تصادفا با آن برخورد می کند نیاید و این روابط به راحتی توسط یک ناظر بی دقت درک نشوند ، اما می توان نظم دیداری موجود در آن ها را با تکرار یک سری از تجربیات حس کرد و نظم بصری ای که ایجاد می کند را طی یک رشته تجربیات مکرر می توان تشخیص داد .
در حقیقت اگر در طراحی که بوسیله سیستم تعیین تناسب تنظیم شده ٬ ابعاد و نسبتهای صحیح نتوانند به طور واقعی و به طریق مشابه توسط همه درک شوند پس سیستمهای تنظیم تناسب چه فایده ای دارند و چرا از اهمیت خاصی در طراحی معماری برخوردار هستند ؟
سیستم های تنظیم تناسب از صورت تعیین کننده های عملکردی و تکنیکی فرم و فضای معماری فراتر رفته استدلالات زیبائی در مورد ابعاد خود ارائه می دهند . آنها با اعطای تناسباتی مشابه و از یک خانواده به اجزاء یک طرح معماری ٬ از نظر بصری می توانند به چندگانگی اجزاء در آن طرح وحدت بخشند .
آنها می توانند احساس نظم را در ترتیب فضاها بوجود آورند و امکان ادامه آنرا افزایش دهند ٬ همچنین می توانند نسبتهایی مشخص بین اجزاء داخلی و خارجی یک بنا بوجود آورند .
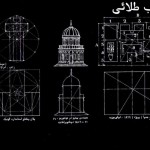
نسبت طلائی و کاربرد آن
مقدمه :
سیستمهای تناسب ریاضی از فرضیه فیثاغورث که می گوید ” همه چیز عدد است ” و از این عقیده که برخی نسبتهای عددی مبین ساختار هماهنگ عالم هستند سرچشمه می گیرند .
یکی از این نسبتها که از عهد باستان تاکنون بکار رفته است تناسبی است که بنام ” تناسب طلائی ” یا Golden Ratio یا golden section شناخته می شود .
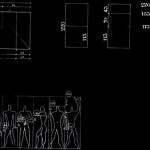
یونانیها به نقش غالبی که تناسب طلائی در تناسبات بدن انسان بازی می کرد پی بردند و با اعتقاد به اینکه هم انسان وهم پرستشگاههای او می بایست به یک نظم برتری از جهان تعلق داشته باشند ٬ همین تناسبات را در ساختمان پرستشگاههای خود منتصویر کردند .
در سده های میانه برای نسبت طلایی مفهومی عرفانی و خرافی قائل بودند.معماران سده های میانه ،رازهای مربوط به پیدا کردن نسبت ها ،از جمله،نسبت طلایی را با دقت از دیگران پنهان می کردند .از جمله اسقف شهر اوترخت به این دلیل که با حیله توانسته بود به روش یافتن نسبت ها در ساختمان کلیسا ها پی ببرد، جان خود را از دست داد.
بسیاری از اثرهای هنری سده های میانه ،و به ویژه در معماری ،با استفاده از قانون نسبت طلایی به دست آمده است.
در بین ستایش گران ویژگی های رمزآمیزعدد طلایی ٬ می توان از لئوناردو داوینچی که آن را ” تقسیم طلایی“می نامیدو کپلر که از اصطلاح”تقسیم آسمانی“برای آن استفاده می کرد ،نام برد .
کپلر (Johannes Kepler 1571-1630) منجم معروف علاقه بسیاری به نسبت طلایی داشت بگونه ای که در یکی از کتابهای خود اینگونه نوشت : “هندسه دارای دو گنج بسیار با اهمیت می باشد که یکی از آنها قضیه فیثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلایی می باشد. اولین گنج را می توان به طلا و دومی را به جواهر تشبیه کرد”.
همچنین کپلر پی به روابط بسیار زیبایی میان اجرام آسمانی و این نسبت طلایی پیدا کرد.
درهمین اواخر نیز لوکوربوزیه ، معمار بزرگ سوئیسی سیستم مدولر خود را بر مبنای تناسب طلائی بنا نهاد و کاربرد آن در معماری حتی تا به امروز نیز ادامه دارد .
امروزه بسیاری از طراحان و معماران بزرگ برای طراحی محصولات خود از این نسبت طلایی استفاده می کنند ٬ چرا که بنظر میرسد ذهن انسان با این نسبت انس دارد و راحت تر آنرا می پذیرد.
تعریف نسبت طلائی :
تناسب طلائی از نظر هندسی می تواند به این صورت تعریف شود :
پاره خطی را در نظر بگیرید و فرض کنید که آنرا بگونه ای تقسیم کنید که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنید. اگر این معادله ساده یعنی را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا 1.61803399 یا 1.618 خواهیم رسید.
تصاویر فایل ها:
خرید آنلاین:
در پایان خرید ، لینک دانلود فایل نمایش داده می شود و به ایمیل شما ارسال خواهد شد. راهنمای خرید و دانلود فایل- فرمت فایل: word – jpg – حجم فایل: 1 مگابایت





با سلام
اینجانب مجید مختاری ارشد معمار و اولین محقق وپژوهشگر معماری نوروساینسیتیک در کشور و خاور میانه هستم که بر روی تاثیر هندسه، علوم ریاضیات و تناسبات روی سیستم مغز و اعصاب انسان کار می کنم.
خواهشمندم در صورت امکان اگر مطالب و مقالات معتبر با ذکر منابع در خصوص این موارد دارید برای بنده ارسال فرمایید تا با حفظ ذکر منبع اصلی جهت استفاده در پژوهشها و تحقیقات کاملا علمی آتی که با دستگاههای پیشرفته تحلیلی و اسکنر مغز و اعصاب کار میشود، مورد استفاده قرار گیرد.
با تشکر و سپاس